es erreurs mathématiques commises par les élèves sont toujours plus ou moins les mêmes. Je ne parle pas des erreurs d’inattention ou de calculs, celles-ci étant d’une importance moindre, sauf si l’on programme le décollage d’une fusée 😉 mais plutôt de fautes de raisonnement ou de présentation des calculs. J’ai répertorié les 6 erreurs à éviter en maths, du moins les plus courantes au collège.
Erreur 1 : Usage abusif du symbole =
Exemple : Calculer A = 4 +2 x 3. Voici ce que l’on rencontre très souvent :
A = 2 x 3 = 6 + 4
FAUX ! 🙁
Ce type de présentation des calculs est très fréquente au collège. L’élève ayant intégré que la multiplication est prioritaire, il calcule 2×3 mais s’empresse de rajouter 4 à la suite de l’égalité. Ce qui donne très souvent : 2 x 3= 6 + 4. Vous l’aurez compris, 2×3 est bien égal à 6 mais PAS à 6+4 ! En mathématiques, l’emploi des symboles doit faire l’objet de la plus grande rigueur.
Cela peut paraitre trivial mais l’expression à gauche du symbole « = » doit être égale à celle qui est à sa droite !
Le mieux est de passer à la ligne pour séparer les étapes intermédiaires de la manière suivante :
A = 4 +2 x 3
A = 4 + 6
A = 10 🙂
On a : AB2= 50. En prenant la racine carrée, on trouve AB ≈7,07.
En utilisant la propriété de Pythagore dans le triangle rectangle ABC, on a :
AB2+ BC2= AC2
Soit AC2= 7,072+ 7,072= 99.9698
FAUX, ce n’est pas la valeur exacte !
La consigne exige ici une valeur exacte. C’est donc que les données le permettent !
Voici le raisonnement correct qui nous conduit à la valeur excate et non à une valeur approchée :
On sait que AB2 = 50
Dans le triangle ABC, rectangle en B on applique la propriété de Pythagore :
AB2+ BC2= AC2
Or AB=BC puisque ABCD est un carré. Donc AB2= BC2=50.
On obtient donc :
AC2=50+50
AC2=100
Soit AC=10 qui est bien la valeur exacte.
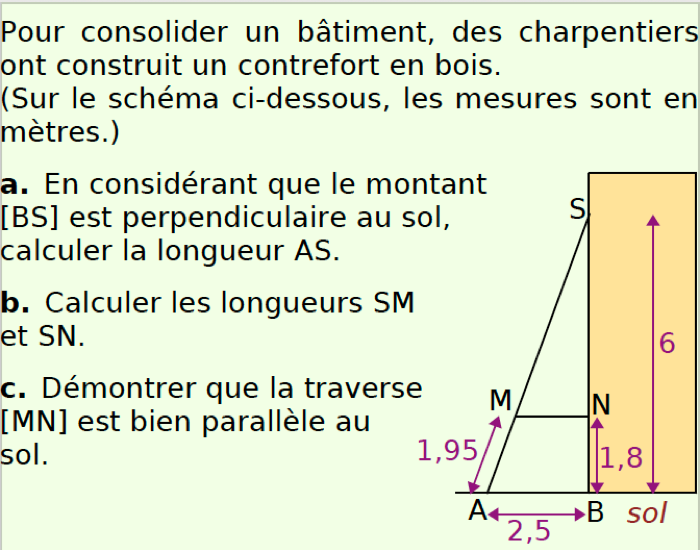
n reconnaissant une configuration de Thalès, l’erreur, certes tentante serait d’appliquer la propriété de Thalès pour calculer SM. Le calcul donnerait 4,55. Le résultat est juste par ailleurs mais le raisonnement est faux, ce qui peut parfois se produire en mathématique ! En effet, pour appliquer la propriété de Thalès il faut impérativement s’assurer que les droites (MN) et (AB) sont parallèles. Or à ce stade de l’exercice, rien ne le prouve. Ici, il fallait utiliser la propriété de Pythagore pour déterminer AS.
D’ailleurs la question c. nous rappelle que a priori les droites ne sont pas supposées être parallèles !
Vérifiez toujours les conditions requises avant d’appliquer un théorème !
a réciproque de Pythagore ou sa contraposée (il en est de même pour la réciproque de Thalès) donne souvent lieu à une rédaction incorrecte sur le plan mathématique. Considérons le problème suivant :
On donne une triangle ABC tel que AB=12 cm, BC=15 cm et AC=6 cm. Ce triangle est-il rectangle ?
Voici le type de rédaction que l’on rencontre souvent :
BC2 =AB2+AC2
152=122+62
225=114+36
225=225
Donc le triangle est rectangle. REDACTION INCORRECTE !
Ecrire une égalité sans aucune phrase l’accompagnant suppose implicitement qu’elle est vraie.
L’erreur est à la première ligne. Lorsqu’on écrit une égalité sans aucune phrase explicative, cette égalité est supposée vrai. Or à ce stade, rien ne prouve qu’on ait égalité puisque précisément on ne sait pas si le triangle est rectangle. Il faudrait rédiger de la manière suivante :
Le côté le plus long est [BC].
Je calcule d’une part : BC2 = 225
Je calcule d’autre part : AB2+AC2 = 114 + 36 = 225
Donc : BC2 =AB2+AC2
D’après la réciproque de Pythagore, le triangle est rectangle en A.
emploi des identités remarquables est très fréquent et ce à n’importe quel niveau. Que ce soit dans le secondaire ou dans le supérieur, il est indispensable de connaître les 3 identités remarquables. Elles permettent de factoriser ou de simplifier les calculs.
Voici ci-contre ces 3 formules qui se démontrent aisément :
Exemple : développer l’expression (a+4)2
Voici ce que l’on rencontre trop souvent :
(a+4)2 =a2 + 42 FAUX 🙁
N’oubliez pas le double produit, voici la bonne réponse :
(a+4)2 =a2 + 2 x a x 4 + 42
(a+4)2 =a2 + 8a + 16
Attention ! le carré d’une somme n’est pas égal à la somme des carrés !
Voici le type de rédaction que l’on voit très souvent :
Etape 1 : Je choisi 4
Etape 2 : Valeur 1 = 1 + 4 = 5
Etape 3 : Valeur 2 = 3 x 5 = 15
Etape 4 : Résultat = 15 – 3 = 12
Etape 1 : Je choisi 7
Etape 2 : Valeur 1 = 1 + 7 = 8
Etape 3 : Valeur 2 = 3 x 8 = 24
Etape 4 : Résultat = 24 – 3 = 21
Dans tous les cas on trouve bien le triple du nombre choisi.
Raisonnement FAUX !
Des exemples, même en très grand nombre, ne prouvent rien mathématiquement.
Le raisonnement est faux. En effet même si nous avions testé 1000 ou même un milliard de valeurs, rien ne prouve que cela fonctionnera pour une autre valeur. C’est une différence fondamentale entre la physique et les maths. En physique, un modèle est considéré comme acceptable tant que l’expérience ou une observation n’a pas prouvé le contraire. En mathématiques, une proposition se prouve de manière générale, le plus souvent en utilisant le calcul littéral.
Voici une rédaction correcte :
Soit a le nombre choisi :
Valeur 1 = 1 + a
Valeur 2 = 3 x (1 + a) = 3 + 3a
Résultat = 3 + 3a – 3 = 3a
3a est le triple de a
Il n’est cependant pas interdit de tester des valeurs, au contraire, cela peut permettre de s’approprier le problème mais en aucun cas ces exemples même en grand nombre de prouveront la véracité d’une proposition. En revanche un seul contre-exemple (comme son nom l’indique il permet de contrer une proposition) suffit pour affirmer qu’une proposition est fausse.
